|
Tesla theory ... ma come funziona la bobina di Tesla? |
|
In questa pagina cercherò di spiegare come funziona una bobina di Tesla. Inizierò l'analisi con il solito circuito RLC serie (universalmente tirato in ballo quando si parla di bobine di Tesla) e poi lo proseguirò con lo stdio di un Tesla Magnifier con la teoria delle linee di trasmissione. Alla fine otterrò anche una relazione che legherà la tensione di uscita a quella di ingresso. Come
funziona la bobina di Tesla? ...
il circuito RLC serie
Se ora si prende excel e gli si fa disegnare l'andamento di Vout in funzione della frequenza, si ottiene che (supponendo R = 1ohm, L = 30mH, C = 10pF e Vin = 1V)
Che vuol dire? "Semplicemente" che, se riusciamo ad alimentare il gruppo LC esattamente alla sua frequenza di risonanza, otteniamo, ai capi dell'induttore, una tensione molto più elevata di quella che viene applicata all'ingresso. Ma non è tutto, perchè, sempre alla frequenza di risonanza, il circuito è, nei confronti del generatore di tensione, un carico perfettamente resistivo (di valore pari alla resistenza R). Fin qui non ho detto niente di diverso da quanto si legge in tutti i libri di elettrotecnica.
Il Tesla Magnifier Il Tesla Magnifier è una particolare implementazione della bobina di Tesla che prevede di alimentare la bobina stessa direttamente ad un estremo. Nella bobina di Tesla classica ci sono due avvolgimenti: un primario (a cui viene fornita l'alimentazione) ed un secondario (dal quale si preleva l'alta tensione). Il Tesla Magnifier invece ha un solo avvolgimento che viene alimentato direttamente da un lato.
E' evidente che se si pensa alla bobina di Tesla come un gruppo RLC serie, il Tesla Magnifier non potrebbe funzionare poichè saremmo di fronte ad un generatore che alimenta un ramo aperto. Invece il Tesla Magnifier funziona (e anzi è quasi una strada obbligata se si vuole lavorare a qualche MHz). Se ne conclude che occorre studiare la bobina di Tesla con un diverso approccio. Come funziona la bobina di Tesla? ... la linea di trasmissione Ma ora facciamo un passo avanti. Prendiamo una qualunque bobina avvolta su un qualunque supporto (che sia un tubo di plastica, un bicchiere di vetro o una bacchetta di ferrite poco importa). Si osserva che la bobina è composta da una certa quantità di filo di rame, avvolto a spirale .... ne consegue che la bobina sarà caratterizzata da
Pertanto la bobina, che per basse frequenze funziona davvero come una bobina, al crescere della frequenza deve essere invece pensata come un circuito a parametri distribuiti:
Un circuito di questo tipo, a rigori, si deve studiare con la teoria delle linee di trasmissione, che in sè non è tanto complicata, il difficile sta nel ricavare tutti i parametri che servono per descrivere la linea e poterla poi studiare. Nel caso della bobina, poichè determinanti sono proprio le capacità verso massa che dipendono da tutto ciò che circonda la bobina stessa (quindi anche da chi effettua la misura vera e propria) bisogna prendere parecchie preacauzioni al fine di avere una descrizione sensata. Per poter studiare cosa succede su una linea di trasmissione, occorre considerare che un segnale elettrico si propaga, lungo la linea stessa, con una velocità finita. Supponiamo quindi di prendere una linea di una certa lunghezza, di chiudere un'estremità su una resistenza R e di alimentare l'altra estremità con un generatore di tensione. Lungo la linea si instaurano quindi due diversi flussi di energia:
Per tener conto di questi due flussi di energia, ci "inventiamo" la tensione diretta Vd e la tensione riflessa Vr. Poichè la tensione diretta Vd si propaga verso il carico, mentre la tensione riflessa si propaga verso il generatore si osserva che, muovendoci dal carico verso il generatore
Questi due fatti si riassumono nella seguente equazione in forma esponenziale (dove x è la distanza dal carico mentre).
Il parametri LAMBDA è la lunghezza d'onda del segnale lungo la linea, mentre ALFA tiene conto dell'attenuazione lungo la linea stessa. E il legame con la velocità di propagazione è all'interno del parametro lambda:
In maniera analoga, esisteranno due flussi di corrente, uno diretto dal generatore al carico, l'altro riflesso dal carico verso il generatore:
Il parametro Z0 è l'impedenza caratteristica della linea ed è legato sia alla struttura geometrica della linea che alle proprietà elettriche dei materiali che la compongono. La tensione riflessa è sostanzialmente causata dal fatto che lungo la linea il segnale elettrico si propaga in un certo modo determinato dalle caratteristiche della linea stessa. Giunto al termine della linea, il segnale si "scontra" con il carico e subisce alcune modifiche nel modo di propagarsi .... si pensi, per esempio, ad una palla da tennis lanciata verso un muro. Inizialmente la palla si propaga verso il muro in una certa direzione e con una certa velocità. L'impatto con il muro altera il moto della palla respingendola in un'altra direzione e con diversa velocità. Per il segnale elettrico, tuttavia, la riflessione è determinata non tanto dalla presenza del carico, quanto, piuttosto, dal fatto che risente di un brusco cambiamento nell'impedenza caratteristica del mezzo in cui si propaga. Infatti l'ampiezza della tensione riflessa è legata alla tensione diretta dal "coefficiente di riflessione":
Chiaramente il coefficiente di riflessione così calcolato è valutato a fine linea, e subisce dei cambiamenti lungo la linea stessa a causa delle rotazioni di fase e delle variazioni di ampiezza delle onde diretta e riflessa. A questo punto abbiamo tutti gli strumenti per iniziare lo studio vero e proprio della bobina di Tesla. Per prima cosa proviamo a calcolare il rapporto fra la tensione di linea V e la corrente lungo la linea I. Tale rapporto ci fornisce l'impedenza vista lungo la linea ad una distanza x dal carico. Riporto direttamente il risultato, risparmiando i vari passaggi necessari.
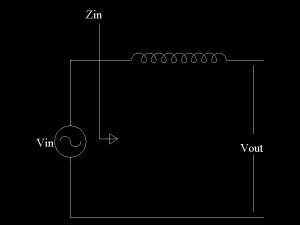
Nel caso della nostra bobina di Tesla, il circuito che dobbiamo studiare è
Si vede immediatamente che la linea di trasmissione, costituita dall'accoppiata fra la bobina e la terra, lavora aperta, cioè è "chiusa" su un carico infinito. Pertanto, applicando la [4], il coefficiente di riflessione vale 1 (e Vr = Vd). In queste condizioni la [5] si trasforma (dopo qualche passaggio) nella
X rappresenta la lunghezza della linea, quindi la [6] fornisce l'impedenza di ingresso della linea al variare della lunghezza. Tuttavia, nessuno vieta di considerare una linea di lunghezza "x": quanto sia x non ci interessa minimamente, basta pensare che sia un certo valore finito. In questa equazione ci sono due parametri (LAMBDA e ALFA) di cui a priori non si conosce il valore (e chiaramente poi bisognerà escogitare un sistema per ricavare tali valori). Per il momento, tuttavia, è interessante valutare cosa succede in un caso ben preciso. Supponiamo che la linea sia lunga esattamente un quarto della lunghezza d'onda:
Sostituendo la [8] nella [6] si ottiene
Infine, poichè la tangente di "pigreco/2" è infinita, si può semplificare e si ottiene il seguente importantissimo risultato
La [9] ci dice che, se riusciamo a far lavorare la nostra bobina in modo tale che la sua lunghezza complessiva sia esattamente pari ad un quarto della lunghezza d'onda, allora l'ingresso della bobina (alimentata come in figura 3) costituisce un carico resistivoil cui valore è dato dalla [9]. Nel caso la bobina fosse avvolta con un filo idea, di resistenza esattamente nulla, allora la linea di trasmissione sarebbe caratterizzata dall'assoluta assenza di perdite, pertanto il coefficiente ALFA sarebbe nullo e la [9] darebbe un risultato esattamente nullo. Più avanti vedremo cosa vuol dire realizzare la condizione [8]. A questo punto proviamo a riscrivere anche la [1] sostituendo la condizione [8] (e ricordando che Vr = Vd) in modo da trovare un legame fra la tensione all'ingresso e la stessa Vd
Scritta così dice ancora poco, ma basta usare una formulina trigonometrica e si ottiene
Da cui infine si ottiene
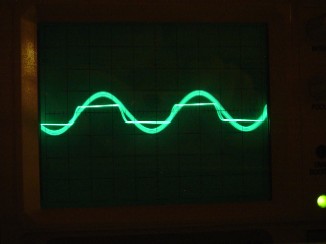
Le equazioni [8], [9] e [10] ci svelano vita morte e miracoli della nostra bobina di Tesla. La [8] fornisce " solo" un legame fra la lunghezza della linea di trasmissione e la lunghezza d'onda. Ma quale lunghezza d'onda? Non certo la lunghezza d'onda nel vuoto (cioè quella che si ottieme dividendo la velocità della luce per la frequenza), ma bensì la lunghezza d'onda all'interno della linea di trasmissione stessa. Infatti la velocità di propagazione del segnale dipende dal mezzo in cui avviene la propagazione, e allo stesso modo la lunghezza d'onda dipende dal mezzo in cui avviene la propagazione. E siccome non sappiamo quanto sia la velocità di propagazione dentro la nostra bobina, non sappiamo tirare fuori niente dalla [8]. Ma fermiamoci un attimo a pensare .... abbiamo preso la nostra bobina e la stiamo alimentando con un generatore di funzioni (e quindi possiamo giocare a nostro piacere con la frequenza). La nostra bobina sarà caratterizzata da una certa lunghezza x. Sappiamo quant'è questa lunghezza x? In realtà no, perchè si tratta della lunghezza vista dal segnale durante la propagazione all'interno della bobina. Al momento non so dire se sia in qualche modo legata alla lunghezza fisica del filo con cui la bobina è avvolta ... probabilmente un legame c'è, ma non è ora il momento di fare congetture (e poi ora possiamo farne a meno). Poi pensiamo alla lunghezza d'onda: un segnale a bassa frequenza ha una grande lunghezza d'onda mentre un segnale ad alta frequenza ha una lunghezza d'onda più corta. Se iniziamo il nostro esperimento con una frequenza di alimentazione molto bassa e piano piano la aumentiamo, sicuramente incontreremo una frequenza per cui si realizzerà la condizione [8]. Tale frequenza può anche essere chiamata "frequenza di risonanza" . E' da notare che, un volta trovala la frequenza di risonanza, la bobina presenterà proprietà simili anche per tutti i multipli dispari della frequenza di risonanza stessa. In definitiva, la [8] ci dichiara l'esistenza di una frequenza di funzionamento che dipende dalle caratteristiche costruttive della bobina. Non ci fornisce il valore di tale frequenza, ma ci assicura che esiste, quindi al limite potremo anche ricercarla per via sperimentale. La [9], ci assicura che, alla frequenza di risonanza, la bobina è un carico puramente resistivo. Anche in questo caso non ci fornisce un numero, ma ci dice che sarà legato all'impedenza caratteristica (che sarà resistiva e potrà essere misurata) e al numero ALFA. Il fatto che sia legata al numero ALFA è estremamente interessante poichè ALFA è legato alle perdite esistenti lungo la linea. Tali perdite agiscono in maniera simile alla resistenza serie di un circuito RLC. Morale, così come il circuito RLC serie alimentato alla frequenza di risonanza presenta un'impedenza puramente resistiva (e pari proprio a R), allo stesso modo, una bobina alimentata alla frequenza di risonanza presenta un carico puramente resistivo il cui valore è legato alle perdite che caratterizzano la linea. E una bobina ideale (avvolta con un filo ideale che presenta una resistenza esattamente nulla) alla risonanza apparirà esattamente come un cortocircuito. Infine la [10] ci dice due cose sulla tensione di uscita. Tensione di uscita? Sì! Tensione di uscita. Infatti dalla [1] sappiamo che la tensione per x=0 (cioè all'uscita della linea) è data da Vd + Vr. E poichè Vr = Vd dalla [4] ne consegue che la tensione al terminale di uscita della bobina è data dal doppio della Vd così come calcolato con la [10]. E la [10] ci dice innanzitutto, a causa della presenza del "-j", che la tensione di uscita è ritardata di 90° rispetto alla tensione di ingresso, che è un'informazione utilissima per poter realizzare i tesla coil "autoaccordanti". Inoltre abbiamo un'indicazione sull'ampiezza della tensione di uscita che risulta essere tanto maggiore quanto più piccole sono le perdite. Ancora una volta in perfetta analogia con il circuito RLC serie, se le perdite (e quindi la resistenza serie) fossero esattamente nulle, la tensiione di uscita sarebbe infinita. Per verificare la validità di queste affermazioni, ho preso una bobina avvolta su un tubo di 35mm, con un totale di 1000 spire e l'ho collegata, come in fig. 3 ad un oscillatore ad onda quadra con ampiezza di 10Vpicco e resistenza di uscita di 50 ohm. Poi ho preso un filo di una trentina di centimetri e ho fatto in modo che passasse vicino al terminale di alta tensione della bobina. Tale filo è poi collegato all'ingresso dell'oscilloscopio. La figura seguente mostra il legame fra la tensione di alimentazione della bobina (onda quadra) e la tensione presente sul filo usato come antenna ad una frequenza inferiore alla f0
Si osserva che il segnale di uscita è praticamente in fase con quello all'ingresso. Per le ampiezze ... per l'onda quadra siamo a 20V/div, mentre per la sinusoide di uscita è 10V/div. Aumentando la frequenza di alimentazione si riesce a beccare la frequenza di risonanza f0. Risultato: uscita in ritardo di 90° sull'ingresso e ampiezza esageratamente più grande (20V/div per la sinusoide)
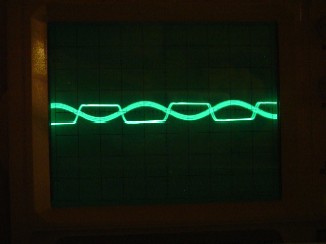
Portando la frequenza di alimentazione molto oltre la risonanza l'uscita è in opposizione di fase rispetto all'ingresso.
Con un'ultima foto voglio dare un ultimo spunto di riflessione. Alla frequenza di risonanza, la bobina funziona anche da ottima antenna e irradia un forte campo elettromagnetico. Quanto forte? Non ho gli strumenti per dare dei numeri sensati, tuttavia la foto seguente dimostra come una lampadina al neon si accenda perfettamente senza essere alimentata ... si tenga presente che la bobina è ancora alimentata con un'onda quadra di 10V di ampiezza........
OK, a questo punto abbiamo un modello abbastanza dettagliato della bobina di Tesla (almeno quando usata nella configurazione Tesla Magnifier, ma cercherò di estendere il discorso alla bobina "classica": quella con i due avvolgimenti primario e secondario perfettamente separati), che però dipende dai parametri ALFA, LAMBDA e Z0. Bisognerà trovare un metodo per ricavare tali parametri almeno in via sperimentale
|
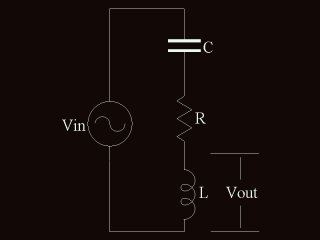 fig.
1
fig.
1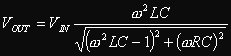
 fig. 2
fig. 2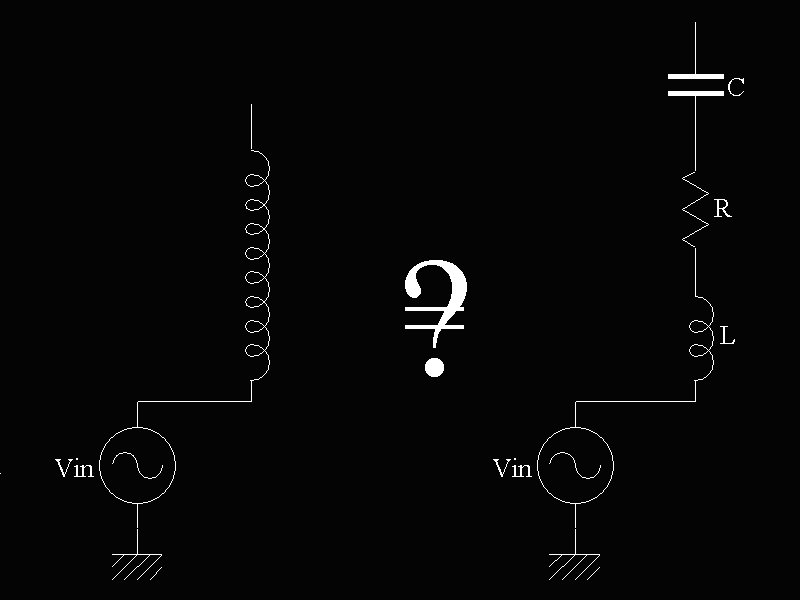 fig
.3
fig
.3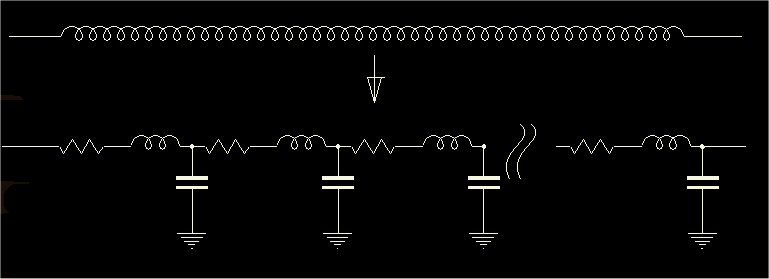
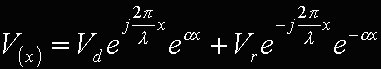 [1]
[1]
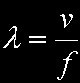 [2]
[2] 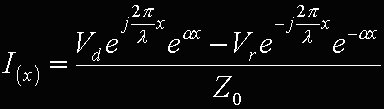 [3]
[3]
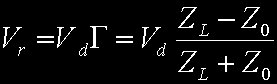 [4]
[4] 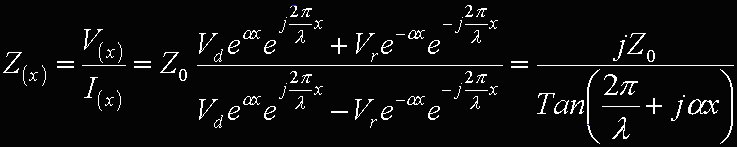 [5]
[5]
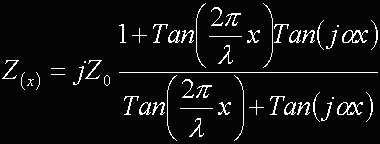 [6]
[6]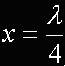 [8]
[8]
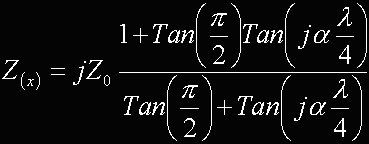
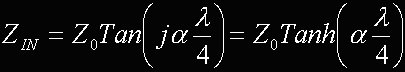 [9]
[9]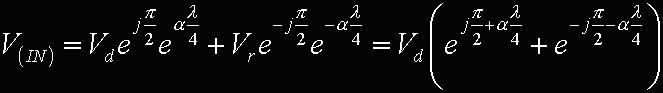
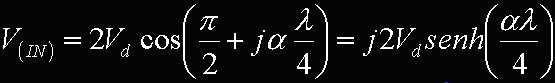
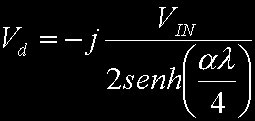 [10]
[10]