|
Tesla theory ... ma come funziona la bobina di Tesla? |
|
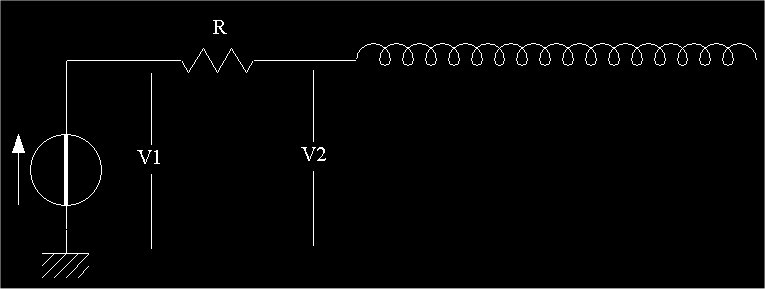
Nella pagina precedente ho cercato di creare un modello teorico che potesse spiegare il principio di funzionamento della bobina di Tesla. Con tale modello sono poi spuntati fuori i parametri ALFA, LAMBDA e Z0 e ci siamo lasciati, appunto, con la promessa di trovare un metodo per ricavare questi valori. Detto fatto, in questa pagina racconterò un metodo sperimentale per ricavare i parametri, fermo restando un punto, che occorrerà approfondire in seguito: tutte le misure, chiaramente, sono fatte alimentando la bobina con piccoli segnali, quindi non c'è la formazione della scarica a corona, nè, tantomento, di archi verso massa. Questo perchè volevo evitare di distruggere gli strumenti di misura a causa delle alte tensioni che si vengono inevitabilmente a sviluppare. Tuttavia può darsi che la scintilla (in forma di scarica a corona) agisca come un carico di una qualche natura che modifica le condizioni di funzionamento della bobina. Pertanto, una volta ottenuti i parametri ALFA, LAMBDA e Z0 con alimentazione a bassa potenza, occorrerà trovare un modo per studiare l'effetto della scintilla e verificare se la sua presenza alteri o meno i parametri trovati. Ma insomma, per ora accontentiamoci di lavorare a bassa potenza. La prima cosa da fare è, senza ombra di dubbio, trovare l'impedenza di ingresso alla frequenza di risonanza. Per questo è sufficiente realizzare il circuito della figura seguente
In ogni condizione di funzionamento, il legame fra le tensioni V1 e V2 è dato da
Invertendola, si ricava la resistenza di ingresso
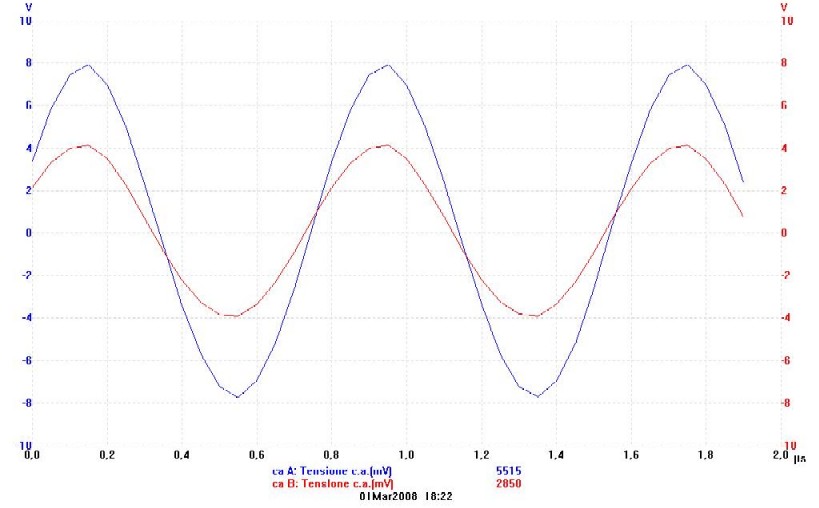
Queste due relazioni valgono sempre, sia che l'impedenza di ingresso sia resistiva, sia che non lo sia. Tuttavia, ho scritto "Rin" perchè stiamo cercando l'impedenza di ingresso alla risonanza che, guarda caso, abbiamo già scoperto essere resistiva. A questo punto occorre prendere generatore di funzioni, oscilloscopio e una bobina, e assemblare il circuito della figura precedente. Ho utilizzato una resistenza da 100 ohm, tanto per fare cifra tonda. Giocando con la frequenza ho centrato la risonanza della bobina ed il risultato è la figura seguente
La traccia blu è la tensione V1, mentre la traccia rossa è la tensione V2. Che si osserva? Il piccolo sfasamento fra le due tensioni è dovuto all'impossibilità di centrare perfettamente la risonanza, tant'è che variando appena la frequenza di lavoro, riesco a portare V2 in anticipo o in ritardo rispetto alla V1, con piccole variazioni di ampiezza. Pertanto considero che le due tensioni siano perfettamente in fase. Questo conferma la correttezza della [9], visto che ci suggeriva un'impedenza di ingresso puramente resistiva. Applicando la [11] si ottiene che in questo caso la resistenza di ingresso è 107 ohm. Prendiamo questo numerino e mettiamolo da parte, ci servirà fra qualche riga. Occorre ora misurare la tensione di uscita per questo ho collegato la bobina direttamente all'uscita del generatore di funzioni e sono andato a misurare la tensione presente su un filo di 5 centimetri posto a 1 centimetro dal terminale di alta tensione. Tale filo, a causa delle inevitabili capacità parassite, si accoppia con il terminale di alta tensione della bobina. Misurando la tensione sul filo con una sonda 1/10 (la cui impedenza di ingresso è tipicamente dell'ordine dei 10Mohm) si ottiene con buona approssimazione la tensione sul terminale di alta tensione. Perchè dico "con buona approssimazione"? Osserviamo la figura seguente ...
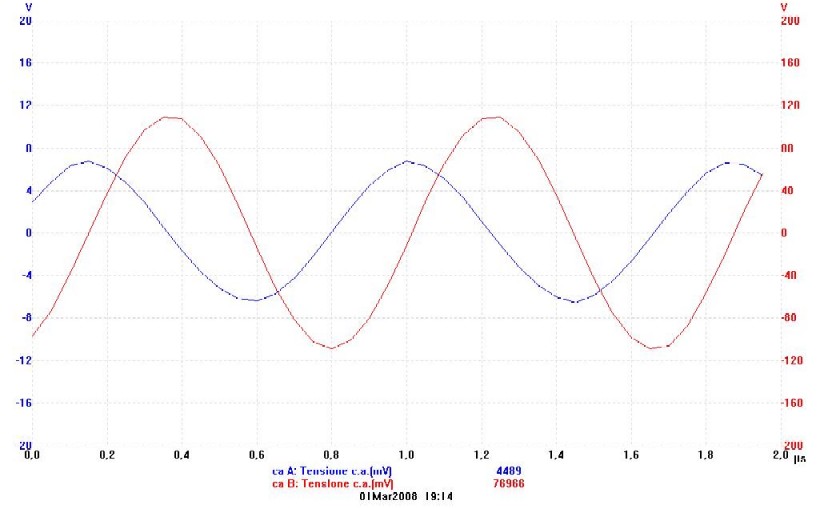
La traccia blu è la tensione di ingresso (per complessivi 4.489V efficaci), la traccia rossa è la tensione di uscita (per 77V efficaci). Si osserva che la tensione di uscita è in ritardo di 90° sulla tensione di ingresso, in perfetto accordo con la [10]. Pertanto, se è vero che la capacità di accoppiamento fra il terminale di alta tensione e l'ingresso dell'oscilloscopio introduce un polo e uno zero, è altrettanto vero che gli effetti di tale polo e zero sono evidentemente trascurabili, almeno sulla fase. Ma se sono trascurabili sulla fase, lo sono anche sull'ampiezza, pertanto se ne conclude che la misura così fatta è abbastanza attendibile. In ogni caso si prenda questa affermazione con le dovute cautele, poichè mi riservo il "diritto" di verificarla. Ora, siccome una misura diretta della tensione di uscità è pressochè impossibile (se non altro perchè il collegamento della sonda dell'oscilloscopio altera le condizioni di funzionamento della bobina e quindi la misura perde di significato), si deve cercare un metodo alternativo. Sono sicuro che la lunghezza della scarica a corona prodotta dal terminale di alta tensione è legata alla tensione prodotta, ma non ho idea del tipo di legame (proporzionale? quadratico? esponenziale? logaritmico? boh?), quindi occorre che mi documenti in questa direzione. Ciò detto, si osserva anche che il rapporto fra la tensione di uscita e quella di ingresso vale circa 17, che possiamo arrotondare a 20 per recuperare l'eventuale attenuazione introdotta nell'accoppiamento co il terminale di alta tensione. A questo punto, combinando i valori ottenuti per l'impedenza di ingresso e per il guadagno di tensione con le [9] e [10] si può ricavare il parametro Z0 e il prodotto fra ALFA e LAMBDA. Ma ci interessa davvero ricavare questi parametri? Si e no: per l'impiego della bobina è necessario costruire un driver e per far funzionare il driver ci serve solo sapere l'impedenza di ingresso della bobina, il guadagno di tensione e le relazioni di fase fra le varie tensioni in modo da poterle eventualmente sfruttare per centrare perfettamente la frequenza di risonanza. Però è anche vero che conoscere questi parametri può aiutarci in fase di progetto per prevedere il comportamento della bobina finita. "Pensa pensa e vedrai, che la soluzione troverai" (citazione da Winni Pooh) ... lo studio fatto fin'ora tratta la bobina di Tesla come se fosse una linea di trasmissione. Pertanto anche i vari parametro Z0, ALFA e LAMBDA sono tipici delle linee di trasmissione. Quindi, c'è qualcosa di male nel dedurre questi parametri ancora una volta dalla teoria delle linee di trasmissione? Non penso proprio. Ecco quindi che i nostri parametri diventano perfettamente noti. La costante di attenuazione ALFA è definita come: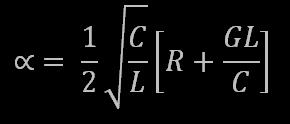 [12] [12]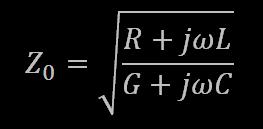 [13] [13]Che nell'ipotesi di linea con piccole perdite (nella quale si trascurano i contributi della resistenza R e della conduttanza G), diventa 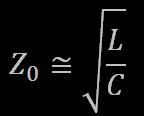 [14] [14]
Infine, è vero che R, L, C sono grandezze per unità di lunghezza, ma .... visto che alla fine sono legate tutte da rapporti, nessuno vieta di rileggerle come
Siamo ora in grado di riscrivere tutte le proprietà della bobina finita a partire dai soli parametri "fisici" R, L, e C. In particolare, ci interessano la resistenza di ingresso e il "guadagno" di tensione Pertanto, riscrivendo la [9] si ottiene: 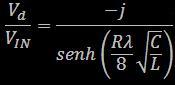 [14] [14]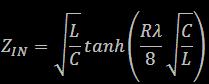 [15] [15]Queste due equazioni ci confermano che:
Arrivati a questo punto occorre trovare un metodo per verificare sperimentalmente le relazioni che abbiamo trovato ed i comportamenti che abbiamo previsto. Per questo ho realizzato un driver "da studio" che consenta di
|
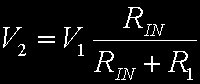
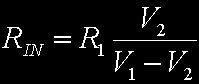 [11]
[11]